Algorithme de Dijkstra et applications
Partie 1 : Graphes, algorithme de Dijsktra et New York
👋 Introduction
L’algorithme de Dijkstra (du nom de son inventeur) sert principalement à trouver le plus court chemin entre une sommet de départ et un sommet d’arrivé dans un graphe orienté pondéré par des nombres réels positifs. Ses applications sont donc diverses et peuvent aller de la simple recherche de chemin dans un graphe à des algorithmes de traitement d’image.
⚖️ Graphe pondéré
Définition formelle
Un graphe est un couple comprenant deux ensembles :
- les sommets du graphe (vertices en anglais)
- les arrêtes du graphes (edges en anglais) dont chaque élément est un couple de sommets (), étant le sommet de départ et le sommet d’arrivé de l’arête.
Remarque : Nous prendrons toujours et supposerons à partir de maintenant que avec la taille de
Chaque graphe peut être pondéré, c’est à dire que l’on associe à chaque arrête une valeur par le biais d’une fonction poids . Dans notre cas l’ensemble d’arrivé est restreint à pour le bon fonctionnement de l’algorithme. Pour simplifier, on suppose aussi que les arêtes sont non orientées, c’est à dire qu’on ne distingue plus de qu’on notera . Voici une représentation d’un graphe non orienté à 6 sommets :
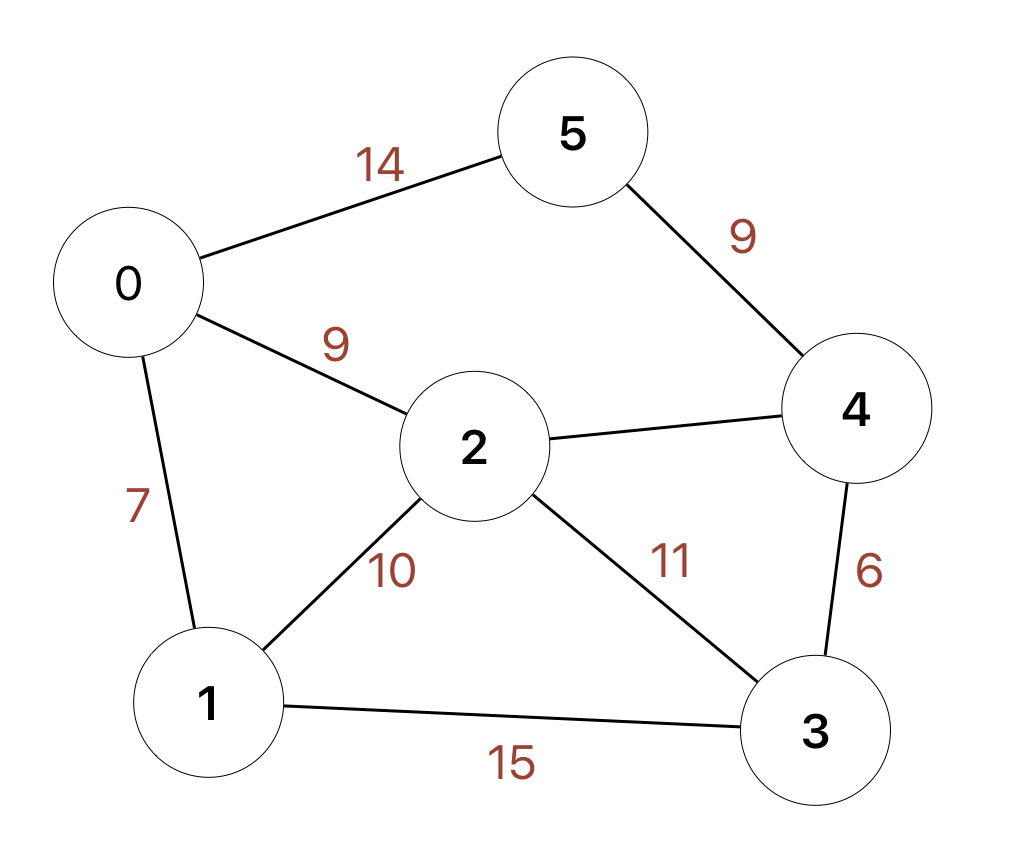
Concrètement, on peut par exemple imaginer que les sommets du graphes représentent des villes et les arrêtes des routes pondérées par leur longueur.
Un peu de vocabulaire
Voisin : et sont voisins si
Degré : Le degré d’un sommet est son nombre de voisins
Chemin : On Appelle chemin de longueur le couple ordonnée des sommets tel que pour tout
Connexité : Un graphe est dit connexe si pour tout il existe un chemin reliant à
Représentations mémoire
On peut stocker les deux ensembles et mais ce n’est pas très efficace. Dans un premier temps et quitte à avoir une fonction d’étiquetage, on considère que l’ensemble est de la forme où est le nombre de sommets du graphe.
Représentation sous la forme de listes d’adjacence
Cette représentation mémoire consiste à stocker les sommets voisins dans une liste de listes par exemple en python :
graphe1_listeadj = [[], [], []]Représentation sous la forme d’une matrice d’adjacence
On peut aussi utiliser une matrice avec pour tout qui vaut si et ne sont pas voisins et le poids de l’arête les reliants si ils sont voisins.
👣 Algorithme de Dijkstra
Une question naturelle se pose alors, étant donné un sommet de départ et un sommet d’arrivé , existe-t-il un chemin de à et si oui, quelle est le plus court. Pour le résoudre, introduisons d’abord une structure de données appelée file de priorité.
File de priorité
Une file de priorité et une structure simple. Elle permet de mettre de côté dans un objet appelée file des éléments en leur associant un numéro de priorité, et d’extraire par la suite l’élément de plus grande priorité. On est doté de 4 opérations appelées primitives sur cette structure:
file_vide()renvoie la file vide
est_vide(f)renvoie un booléen indiquant si la filefest vide
enfile(f, x, p)qui étant donnée une filef, un élémentxet une prioritép, enfile l’élémentxdans la filefavec la prioritép(mais ne renvoie rien)
defile(f)renvoie l’élément de plus haute priorité dans la filefet le supprime de cette file
À noter que les deux dernière fonctions on des effets de bords. Leur appel modifie f quand bien même enfile ne renvoie rien.
Algorithme de Dijsktra
L’algorithme de Dijkstra est alors le suivant. On commence par une initialisation :
- on initialise un tableau
deja_traiteavec les sommets qui ont déjà été traités. Ce tableau est un tableau de booléens tous initialisés àfalse. - On initialise un tableau
precde taille rempli de qui servira à reconstruire le plus court chemin entre et - On initialise un tableau
distde taille qui stocke la distance du plus court chemin découvert jusque là entre le sommet de départ et chaque sommet. Ce tableau rempli de sauf pour le sommet de départ dont la valeur image vaut - On initialise une file de priorité vide dans une variable
f - On enfile dans cette file
fle sommet de départ avec une priorité
On va alors itérativement défiler l’élément de plus grande priorité de f, et si il n’a pas encore été traité, mettre à jour la distance dist des ses voisins au sommet de départ ainsi que prec si nécessaire.
Voici un code python de l’algorithme :
def dijkstra(liste_adj, starting_point):
# Initialisations
n = len(liste_adj)
f = file_vide()
enfile(f, starting_point, 0)
pred = [-1 for _ in range(n)]
dist = [float("inf") for _ in range(n)]
dist[starting_point] = 0
deja_traite = [False for _ in range(n)]
# Le traitement
while not est_vide(f):
u = defile(f)
if not dejaTraite[u]:
for (w, v) in liste_adj[v]:
if not dejaTraite[v] and dist[u] + w < dist[v]:
dist[v] = dist[u] + w
pred[v] = u
enfile(f, v, dist[u] + w)
dejaTraite[u] = True
return dist, pred🗽 Application à la recherche du plus court chemin dans New York
Donnons nous le graphe de New York :
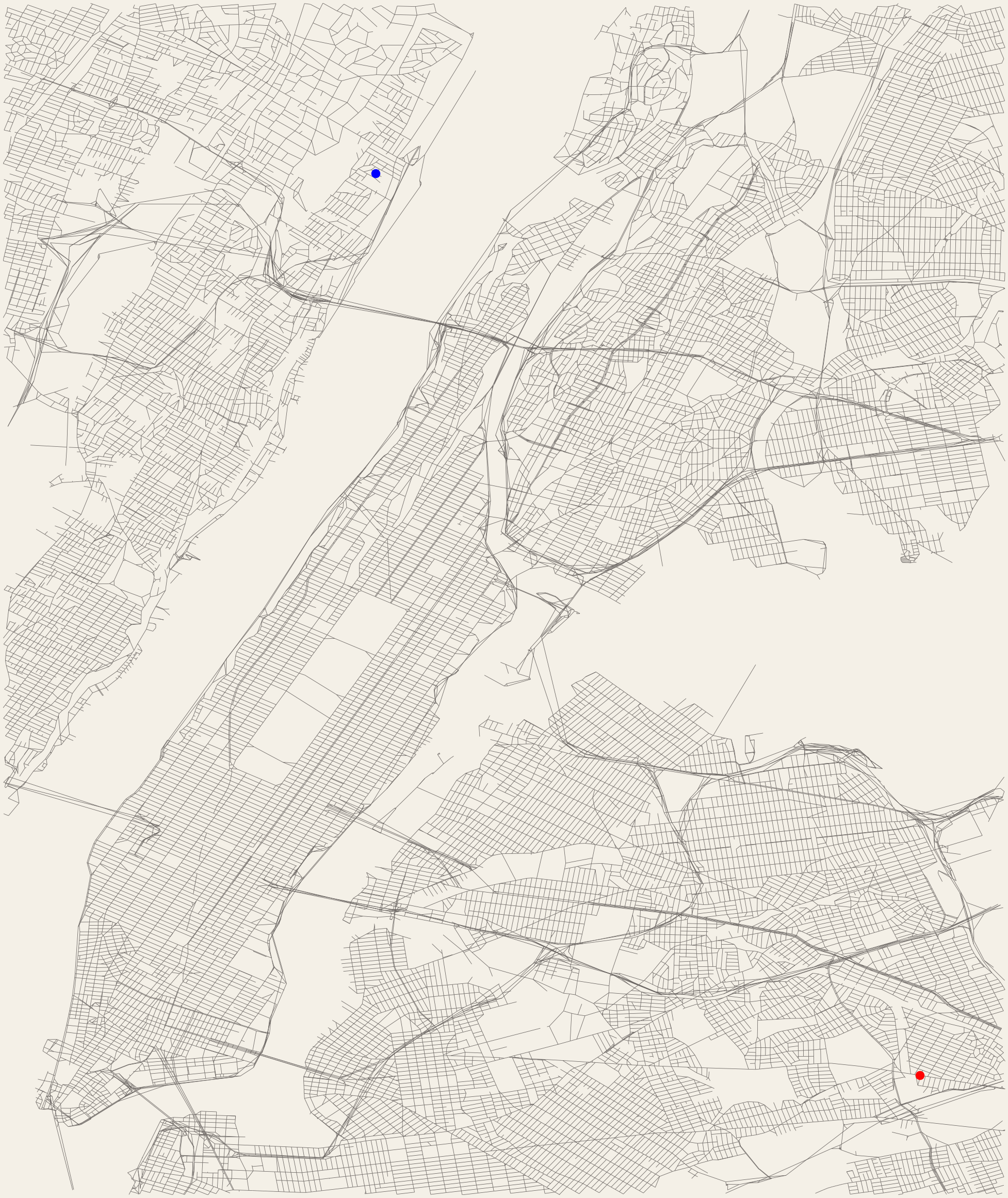 Oui il s’agit bien d’un graphe, juste beaucoup plus grand. Chaque intersection représente un sommet et chaque route une arête pondérée par la distance de celle-ci. On peut alors se donner deux sommets, un de départ c’est le point bleu du graphe, et un d’arrivé, c’est le point rouge. L’algorithme de Dijkstra et la reconstruction nous permettent alors de trouver le plus court chemin entre le sommet de départ et d’arrivé :
Oui il s’agit bien d’un graphe, juste beaucoup plus grand. Chaque intersection représente un sommet et chaque route une arête pondérée par la distance de celle-ci. On peut alors se donner deux sommets, un de départ c’est le point bleu du graphe, et un d’arrivé, c’est le point rouge. L’algorithme de Dijkstra et la reconstruction nous permettent alors de trouver le plus court chemin entre le sommet de départ et d’arrivé :
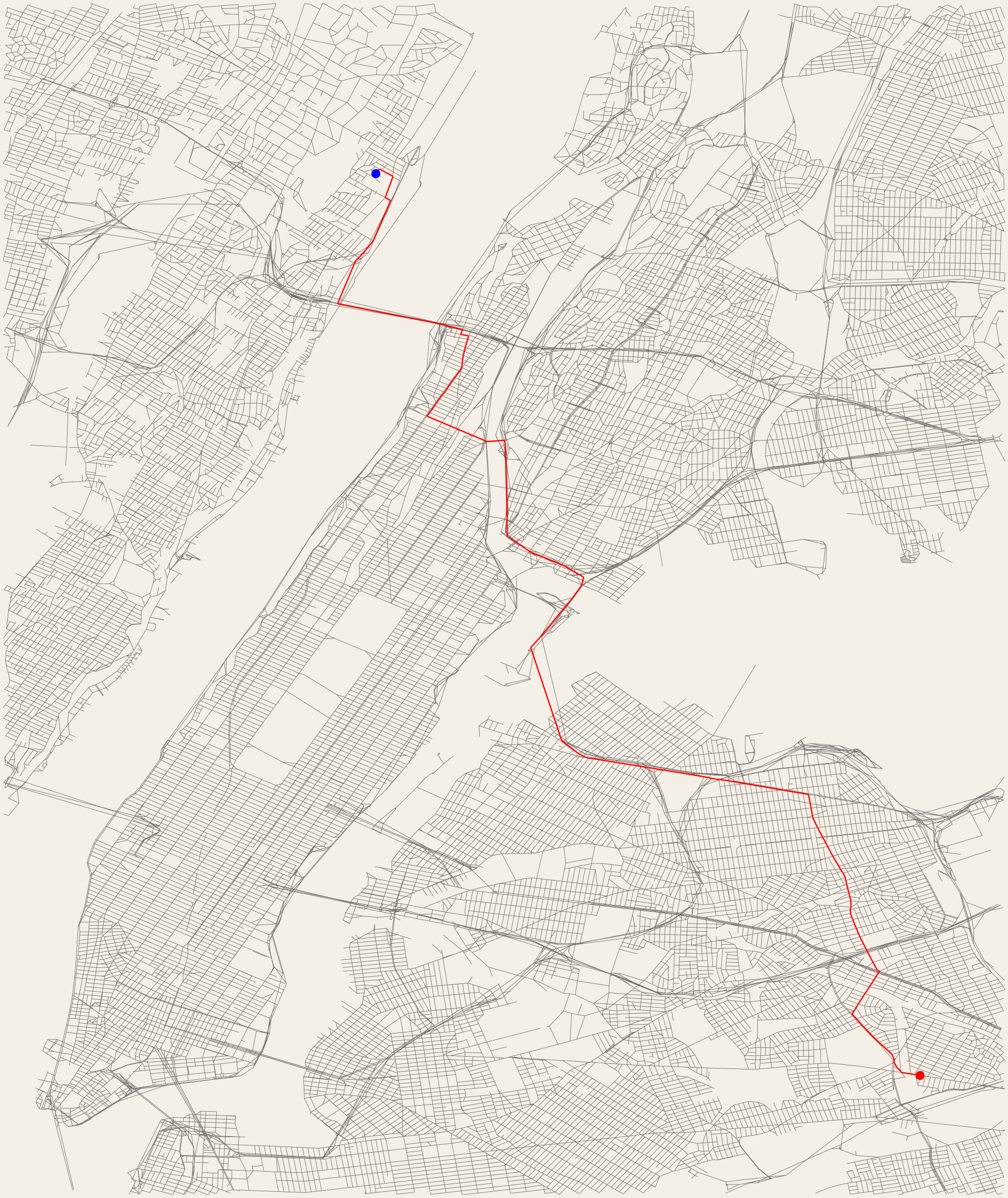
Voilà, on a pu coder un petit GPS !!